Estimando el Cabe

Hemos tratado en otras entradas los parámetros de interés para el estudio del río, uno de ellos es su anchura. La distancia que hay entre dos orillas es una medida que de forma tradicional se incluye en los problemas de semejanza o de trigonometría en las clases de matemáticas como aplicación del estudio de triángulos rectángulos.

Aunque hoy en día tenemos medios tecnológicos para hacer esta medición de forma rápida hemos pensado que es interesante hacer una práctica de medición indirecta al estilo tradicional, incluyendo la construcción de un rectángulo a partir de dos triángulos con la "cuerda de doce nudos" tal como hacían los egipcios. La comprobación del resultado geográfico se ha hecho utilizando el visor SixPac, y el resultado matemático utilizando una simulación con geogebra.

triángulo pitagorico from Angel on Vimeo.

Los estándares asociados están en todos los cursos de secundaria, pero en especial en los bloques de "Procesos, métodos y actitudes" y "Geometría" de segundo y cuarto de ESO. Hemos seleccionado uno de cada bloque y curso para mostrar la relevancia de esta actividad [1].

Estándares de 2º de ESO (LOMCE Galicia)

• MAB1.6.2. Establece conexións entre un problema do mundo real e o mundo matemático, identificando o problema ou os problemas matemáticos que subxacen nel e os coñecementos matemáticos necesarios.
• MAB3.1.1. Comprende os significados aritmético e xeométrico do teorema de Pitágoras e utilízaos para a procura de ternas pitagóricas ou a comprobación do teorema, construíndo outros polígonos sobre os lados do triángulo rectángulo.

Estándares de 4º de ESO (LOMCE Galicia)

• MAPB1.11.4. Recrea ámbitos e obxectos xeométricos con ferramentas tecnolóxicas interactivas para amosar, analizar e comprender propiedades xeométricas.
• MAPB3.1.4. Calcula medidas indirectas de lonxitude, área e volume mediante a aplicación do teorema de Pitágoras e a semellanza de triángulos.

Estimando el ancho del río Cabe ...

RÚBRICA para evaluar la actividad: enlace

Publicación de la actividad: MathcityMap

La actividad que planteamos en esta entrada se ha publicado en el portal MathCityMap asociado al proyecto MoMatrE (Mobile Math Trains in Europe), un programa Erasmus+ que conjuga rutas matemáticas con la utilización de  teléfonos móviles. El objetivo principal es proporcionar una herramienta colaborativa al profesorado que quiera realizar paseos matemáticos con su alumnado o actividades dentro de una ruta.

Está coordinado por la Universidad Goethe de Frankfurt y entre sus socios está la FESPM (Federación Española de Profesores de Matemáticas) que recientemente ha realizado un seminario federal sobre este tema para coordinar las tareas a nivel nacional [2].

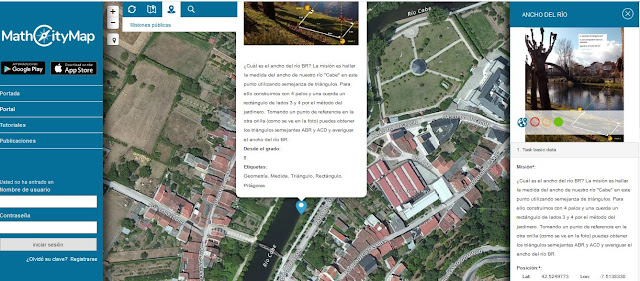Captura de la web con la publicación https://mathcitymap.eu/es/portal-es/?show=task&id=2993

Webs consultadas

[1] Currículo de 2º y 4º de ESO Matemáticas
Matemáticas Orientadas ás Ensinanzas Académicas
Matemáticas Orientadas ás Ensinanzas Aplicadas  
[2] Proyecto ERASMUS+ sobre rutas matemáticas por Europa
http://www.momatre.eu/
https://mathcitymap.eu/es/ 
http://www.fespm.es/La-FESPM-participa-en-el-proyecto